生態系管理の逆理

松田裕之（東大海洋研）

まつだひろゆき

　生物間の間接的な相互作用はしばしば直感に反する効果を及ぼす。多様な生態系を維持することは必ずしも持続可能な漁業に結びつかない。生態系管理にとって、最近の群集生態学の成果は思わぬ難題を突きつけている。

生態系の間接効果

　一つの生態系に属す種は、すべて赤い糸で結ばれている。ある生物にとって、捕食、寄生、住み込み関係や共通の資源を巡る競争関係などによって直接関係する生物種はそれほど多くはないかも知れない。しかし、種ＡがＢと関係し、ＢがＣと関係すれば、ＡとＣは直接関係しなくても、Ｂを介して間接的に関係がある。種Ｃの個体数が増えれば、種Ｂの個体数が変化し、それによって種Ａの個体数も変化する。このようなＡとＣの関係を間接効果(indirect effect)という。

　３種だけの関係でなく、もっと多くの種が介在するすべての関係は間接効果を生じる。同じ生態系に属する種は他種と何らかの直接的な種間関係を持ち、間接的にすべての種が関係を持っている。

　たとえば海鳥や海獣の捕獲、混獲が生態系に及ぼす影響は、複雑な生物群集の食物網を考えた場合、捕食者を獲るとその餌生物も減少するとか、ある種が減ったのにその競争種まで減ってしまうとか、直感に反する結果をもたらす恐れがある。これは食物網の密度変化を通じた間接効果(density-mediated indirect effect)と呼ばれている。

　最も単純で典型的な間接効果の例は、巻き添え競争(apparent competition)である。^{[, ]}これは同じ天敵に狙われる２種の被食者の関係である。一方の被食者が増えればそれを食べる天敵が増え、天敵が増えれば他方の被食者の食害が増える。２種の被食者が直接餌を共有したり、住み場所を巡って競合すれば競争関係にあるが、そうでなくても、２種の被食者は間接的な競争関係にあるというのが巻き添え競争の主旨である。

　植物とそれを食べる草食者、さらにそれを食べる肉食者のように、３つの栄養段階からなる関係でも、植物と肉食者の間に間接効果が生じる。植物が増えるとそれを食べる草食者が増え、結果的に肉食者も増えると期待できる。逆に、肉食者が増えると草食者が減り、そのため植物が増えると期待できる。野菜に害虫がついて被害が出るとき、その害虫を食べる寄生バチのような天敵を導入することで、害虫の被害を防ぐことが期待できる。ところがこの３栄養段階系に殺虫剤をまくと、殺虫剤は害虫だけでなく、その天敵も殺してしまい、かえって害虫が増える心配さえある。^[]

　このような間接効果は、数学的には群集行列の逆行列という形で表すことができる。^[]詳しい数学的説明はここでは省き、簡単な例で示すことにする。

　いま、群集内の種iの個体数をN_iとする。その個体数変化dN_i/dtがdN_i/dt = [r_i+a_i1N₁+a_i2N₂+...+a_isN_s]N_i と表せるとする。ここでr_iは種iの１個体が単独で生きているときの個体数増加率(負なら減少率)、a_ijは種jの１個体が種iの増加率に与える影響を表す定数である(競争関係なら負、捕食関係なら一方が正で他方が負)。

　各種が定常状態にあるとき、個体数が変化しないのだからこの個体数の時間変化を表す連立微分方程式(力学系)の右辺は0である。これをN*=(N₁*, N₂*, ..., N_s*)と表すことにする。このとき、{a_ijN_i*}をi行j列成分とする行列を群集行列という。ここではCと表す。

　種iとjが直接関係を持たないなら、a_ijN_i*は0である。群集内である生物が直接関係をもつ種は必ずしも多くはない。群集行列のほとんどの要素は0である。a_ijN_i*=0とすれば、種jが数を増やしても減らしても種iには直接の影響がない。

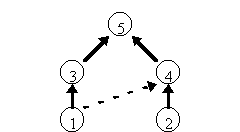
　たとえば図 1(表 1)のような５種の群集模型を考える。上から順に種１から５までのr_iとa_ijを示している。これは種１と２が被食者で、それぞれ種３と４に食われ、３と４が高次捕食者５に食われる状況を表す。さしあたり種１から４へ向かう点線はないものと考える(これについては後で考慮する）。定常状態の個体数と群集行列を表 2に示す。種間関係は全部で10通りあるが、そのうち６通りが直接関係なく、0になっている。たとえば種１と５は直接関係ない。

　ところが、種１が増えると種３が増え、結果的に種５も増える。種３が増えるから先ほど述べた巻き添え競争の関係で種４が減る。種４が減ればその被食者である２が増える。このように、群集内のすべての種は間接的に影響を及ぼしあい、無関係ではない。

　その様子は、表 3に示した群集行列Cの逆行列に負号を付けた行列 -C^-1で定量的に表すことができる。この行列の第i行第j列成分は種jが増えたときに巡り巡って種iがどの程度増えるか減るかを表す。たとえば第4行第1列成分が-0.003とあるのは、種１が増えると種４が少し減ることを表している。群集行列の要素に0(直接効果のない対)が多くても、その逆行列が0になることは稀である。

　種iとjを結ぶ経路が１通りしかないなら、その間接効果は概ね直感的に理解できる。ところが高次捕食者５が種３と４に加えて被食者２も食べる雑食者だとすると、種５が増えたときの種２に与える影響は何とも言えない。天敵が増えることによる直接の被害と、種４が減るために種２が利益を得る間接効果のどちらが大きいかはa_ijの値による。こうして、少し複雑な生態系では、天敵が減ってもその被食者が増えるとは限らない。第３，第４の種を介した間接効果の方が大きいかもしれないからだ。

　そして、食物網の構造が観察から分かっても、a_ijの値を定量的に評価することは難しい。その値が変わると、間接効果は符号も変わる。Peter YodzisはBenguella生態系の食物網を用いて、群集行列の要素の値を変えて間接効果を調べてみた。その結果、直接効果から予測される影響通りの結果になる種間関係は全体の四半分、その反対の効果を持つ関係も全体の四半分、正負が定まらない関係が全体の半分ほどあるという結果が得られた。^[]表 1の食物網ではそう簡単に定性的な結果は変わらないが、図 1の点線の関係が存在するときには、間接効果の大きさにより種１と２，種１と４の関係は正にも負にもなる。食物網が複雑なほど、捕食関係の強さが少しでも変わると予想もつかない影響が現れる。^[]この解析は私のホーム頁(http://ori.u-tokyo.ac.jp/~matsuda/kaiyo98.html)上にあるMathematica? 3.0ファイルで計算することができる。関心のある読者はぜひ確かめられたい。

　漁業管理においても、海獣を駆除しても彼らが餌としている魚が増え、漁獲量が増えるとは限らない。特に海獣は多くの餌を利用しており、複雑な食物網の高次捕食者である。

　たとえば、２種の被食者が競争関係にあり、種間競争が強く、どちらか一方しか存続できない関係にあるとき、共通の捕食者がいることで共存できる場合がある。これを捕食者による被食者の共存(predator-mediated coexistence)という。R. T. Paineが15種類の動植物がいた潮間岩礁帯でヒトデを取り除いたところ、ムラサキイガイ１種が優勢になって7種が駆逐され、多様性を減らした古典的な実験がある。^[]このように競争する２魚種を漁獲する場合、理論的には漁獲率を上げた方がむしろ資源量が増える可能性が示唆される。

多様性と安定性の逆理

　生態系の中にはたくさんの種が存在する。生物多様性(biodiversity)は国際条約によって保全することの重要性が認知され、保全生物学(conservation biology)という新たな学問分野も生まれた。^[]

　しかし、多様な生物がいることに何の価値があるのか、必ずしも具体的に明らかにされたわけではない。1950年代にC. Eltonは、熱帯雨林のような多様な群集の方がそれぞれの種の個体数が安定に維持され、絶滅しにくく、病害虫が大発生しにくくなると主張した。けれども、この一見もっともらしい｢多様な群集ほど安定である｣という仮説は、理論的にも実証的にも必ずしも成り立たないことがわかってきた。^[]私はこのことを｢多様性と安定性の逆理｣と呼んでいる。^[]

　この逆理には二つの意味がある。一つは、多くの種からなる生態系ほど、すべての種が共存する可能性が少ないという、｢多様性と共存可能性の逆理｣である。これは前節で紹介したようなLotka-Volterraの数理模型から導かれる。このdN_i/dt = [r_i+a_i1N₁+a_i2N₂+...+a_isN_s]N_i の共存定常状態は、右辺の括弧内が0になる連立方程式で得られる。r_iやa_ijが無作為に選ばれた値をとるとすれば、解N_i*は正になることも負になることもある。その頻度が大まかに半々だとすれば、n種の系がすべて共存する定常状態をもつ確率は1/2ⁿである。つまり、種数が多いほどすべてが共存する確率は少ない。

　第２の逆理は、種間相互作用が絡み合った複雑な系ほど定常状態が不安定になり易いという、｢複雑性と安定性の逆理｣である。群集の複雑さ(complexity)は１種が平均して何種と直接相互作用をもつかで評価する。定常状態は群集行列がすべて負の固有値をもてば、局所的に安定である。対角要素a_iiN_i*は種内密度効果により負である。もしもそれ以外の要素がすべて0なら、固有値は対角要素に等しく、群集は安定になる。ところがそれ以外の要素が0からはずれるほど、また0でない要素が多いほど、正の固有値の出現頻度が高くなる。だから、複雑な群集ほど不安定になりやすくなる傾向がある。

　以上が｢多様性と安定性の逆理｣の直感的な説明である。この議論は、群集構造が種間の無作為な捕食、競争、双利関係の組み合わせで生じ、相互作用の強さa_ijが無作為な値を採ることを前提にしている。ところが実際の生態系では、捕食者は無作為に食べる餌を選ぶのではなく、大きさや住み場所などの理由があって選んでいる。群集構造全体にも何らかの規則性があるはずである。^[]また、力学系の局所安定性と生態学で意味する安定性が同じものとは限らない。浮魚群集だけでなく、熱帯雨林の生態系でも非定常状態にありながら共存しているという認識が広まりつつある。

生態系管理の秘訣

　人類は、このような間接効果で結ばれた生物資源をどのように利用し、管理すべきだろうか。21世紀の水産学は、この途方もない難題に真正面から取り組まなくてはいけない。20世紀の水産学が定常環境を仮定した単一資源の管理に失敗し、多くの魚種を乱獲状態に陥れてきたのに、生態系全体を管理することができるのだろうか。

　20世紀の水産学が乱獲を防ぐことができなかったのは、おそらく、科学としての水産資源学の未熟さが原因ではない。たしかに定常環境下での平衡状態を仮定したり、他の生物の状態と切り離して個々の魚種の再生産関係を仮定した理論は未熟であり、定量的に高度な管理を行うに耐えるものではなかった。けれども、管理が失敗した最大の原因は、網目を大きくしたり、漁獲努力を制限したり、減った魚を禁漁にするという素朴で明快な方策すら実行できなかった点にあると思われる。

　このような理論的には単純な管理方策すら実行できない状況が続く限り、生態系管理など夢のまた夢かもしれない。しかも先ほど述べたように、生態系の間接効果はどんな方策がどんな結果を生むかがわからない。ある数理模型では望ましい結果が予想される方策も、想定していない種を加えたり種間相互作用を考慮したり、パラメタの値を少し変えるだけで正反対の結果が生じる恐れがある。さらに、上記の結果は群集構造を固定した定常状態の変化だけを議論しており、実際の群集はほとんどの場合、より可変的で、しかも定常状態に達することのない非定常系にある。

　私見では、複雑な生態系模型を作って生態系全体を管理することを試みても、実りある成果は得られないのではないかと思う。国際漁業交渉の舞台などでは、各国が互いに相手により実効性のある管理方策を求めて交渉する。このような席では、より説得力ある解析結果を示すためにより複雑な生態系模型が威力を発揮する傾向があるように思われる。それは軍拡競走(arms race)と同じく、実りのない共倒れへの道かもしれない。

　むしろ、単純で直感的に分かりやすい方策こそ、実効性が期待できる。上記のように直感に反する結果が頻出することには注意すべきだが、未成魚を保護し、減った魚は禁漁にし、一定の漁獲圧をかけるのではなく資源水準により漁獲圧を調整し、低い栄養段階の魚種を多く利用するという理屈の上では単純な方策が有効であると思われる。もちろん、これを実現するには魚種や大きさを選んで漁獲する技術の開発が必要である。^｢｣

　しかし、現在の世界の研究者の大勢は、複雑系(complex system)を礼賛し、(それとは本来別のことだが)より複雑な数理模型を用いて漁業管理を試みようとしている。管理方策を立てる上で単純な方策を推奨する動きもあるが、^[]まだ少数派であろう。この傾向があと何十年続くかは不明である。

生態系管理の逆理

　さらに問題なのは、持続可能な漁獲量を増やすことと、生物多様性を維持することの間の葛藤である。各種を独立に考える限り、その生物資源を根絶すれば持続可能な利用はできない。その意味で、持続的利用(sustainable use)と多様性保全(biodiversity conservation)の間に矛盾はなかった。しかし、生態系全体から得られる持続可能な漁獲量を増やすことは、必ずしも個々の種を保全することには繋がらない。端的に言えば、浮遊生物食浮魚類(plantotrophic pelagic fish、被食者)とそれを食べる魚食性魚類(piscivorous fish、捕食者)を同時に利用する場合、捕食者を根絶して被食者だけを利用する方が持続可能な総漁獲量が増える可能性がある。これは次のような簡単な数理模型で説明できる。

　dN/dt = (r - a N - b P) N - f N
　dP/dt = (-d + e b N) P - g P
ここでNとPはそれぞれ被食者と捕食者の個体数(時間tにより変動する変数)、rとdはそれぞれ被食者の内的自然増加率と捕食者の死亡率、aとbはそれぞれ被食者の密度効果の強さと捕食者に食べられやすさを表す係数、eは捕食者が被食者を食べたときのエネルギー転換効率で1kgの被食者を食べた捕食者資源がekg増えることを表し、fとgはそれぞれ被食者と捕食者に対する漁獲率を表す定数である。被食者と捕食者の定常個体数はそれぞれN*=(d+g)/beとP*=(ber-ad-ag-bef)/b²eである。

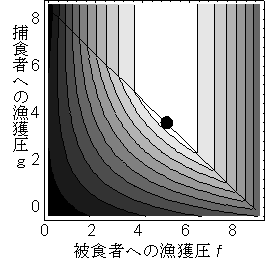
　被食者と捕食者の漁獲量はそれぞれfN*とgP*だが、単位漁獲重量あたりの単価は一般に両者で異なる。被食者の単価を１としたときの捕食者の相対的な単価をpとすると、総漁獲高CはfN*+gpP*と表すことができる。r=10, a=b=d= e=p=1のとき、f=5, g>4で総漁獲高は最大になる。このとき、捕食者は絶滅し、被食者資源水準はN*=5となる(図 2)。捕食者の単価pが十分高ければ、逆に被食者は保護し、捕食者だけを漁獲する方が全漁獲量が高くなる。

　捕食者がいなくなれば、その分被食者の資源量が増える。捕食者に対する漁業としては持続可能ではないが、被食者を持続的に利用することができる。この例では、両者を共存させながら両種とも利用するより、被食者だけを利用した方が漁獲高が増える。

　一般に、捕食者の単価は被食者より高い。100kgのイワシを餌にして15kgのハマチを養殖すれば、そのハマチから得られる利益の方が大きい。つまり、ep>1の状況が多い。けれども、国民により多くの蛋白源を供給するという観点からは、イワシを直接人間が食べた方が効率的である。それなら、イワシのような栄養段階の低い魚種を利用し、それを食べる捕食者は生態系にいない方がよいことになる。

　上記のような単純な数理模型からは、多くの栄養段階が共存し、いろいろな栄養段階の魚種を利用するよりも、高次捕食者を根絶して生態系を単純にする方が効率的である。しかし、これは明らかに望ましい姿ではない。これを｢生態系管理の逆理｣(paradox of ecosystem management)と呼ぶことにする。

　我々は、まだ多様な生態系を持続的に利用することの意義を理論的に説明することができない。この逆理を解決しない限り、多様性の保全は持続可能な漁業と乖離した要求になる。また、多栄養段階の魚種を利用することは商品の多様性を増やす以外に意義がないことになる。

　本稿では、最近の群集生態学の研究成果をもとに生態系管理を行う上で問題となるであろう点について、私見を述べた。執筆の機会を与えていただいた水産庁西海区水産研究所の堀川博史氏と、今年東京大学海洋研究所を退官された沖山＃＃教授に感謝する。

表 1　５種の群集模型のr_i(左の列)とa_ij(右の行列)

表 2　図 1の食物網の定常個体数N_i(左の列)と群集行列C(右の行列)

表 3　群集行列Cの負号を付けた逆行列 -C^-1

図 1　簡単な食物網の例

図 2　被食者と捕食者への漁獲努力fとg(それぞれ横軸と縦軸)と定常状態での全漁獲量の等高線図。色が薄い場所ほど漁獲量が高く、黒丸が最高になる。

参考文献