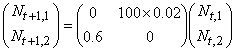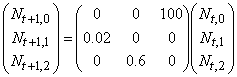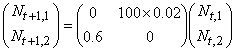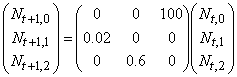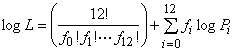｢ゼロからわかる生態学」第1刷からの修正　 　更新　

• P3、28行目：　化学同人　→　東京化学同人
• P8、24行目：　・・・無性生殖を始めることもある．これを遺伝子浸透という．この場合，・・・わかってきた．昔は・・・　→　・・・無性生殖を始めることもある．この場合，・・・わかってきた．このように，雑種が元の集団と戻し交配することで，一方の集団から他方の集団へ遺伝子が流入することを遺伝子浸透という．昔は・・・　（以下１行増える）
• P8､17行目:ヒトを含む多む動物　→　ヒトを含む多くの動物
• P39(1.4)式、w(t)＝ｂ（L/ａ）^3/2Ｎ(t)^-3/2　　　　【N(t)べき指数は-3/2でした】
• P47第2段落4行目：0.2　を　0.02、
• P47第2段落7行目：100×0.2を100×0.02
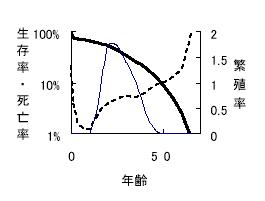
• P55：図2.7(a)を下記に差し替える（細線と破線を入れ替える)。
  
• P67　(2.7)式：
  
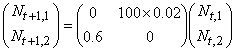
• P68　(2.10)式：
  

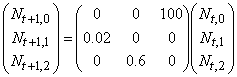
• P68　(2.10)式下３行目：「書き直すと，Ｎ_t+2,2＝100×0.02×0.6×N_t,2＝」
• p.69　（2.15）式：１＝2×0.2／λ²＋10×0.08／λ³
• p.69　（2.16）式：「N_t,a = (l_a/l_a-1)N_t-1,a-1/λ ただしa > 1」
• P.73　14行目：「補足２．６　サイズ構造の数理モデル」（小見出し名変更）
• P.81　15-16行目：「右上側では種１が減り，左下側では増えることを意味する．」
• P.87　図3.4の説明：(i)密度依存的繁殖が１カ所に集まってから生じる場合（太線）と(ii)密度依存的繁殖が１カ所に集まる前に各生息地で生じる場合（細線）．(i)の太線は種Aだけ存続するが、(ii)の細線は2種が共存する．本文参照
• P.97、図3.8説明：タイプ1，2，3がそれぞれ直線，細線，太線．
• P102、10行め：反応PN₁N₂でもなく，1被食者あたりの被食リスクPN₂である．
• P.107、図3.12：対称性のゆらぎ(a)，定向性非対称(b)，
• P.108, 5行目：　dN_idt →dN_i/dt
• P.110、式(3.4)：　dN_i/dt →　dN₁/dt
• P.112、式(3.7)：(dN₂/dt)/N₂ =r₂ [1 - (N₂ + a₂₁ N₁)/K₂] = r₂ (K₂ - a₂₁K₁) K₂ ☆3文字訂正
• P.117、2行目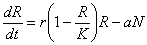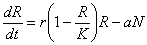： 　→R　 　☆最後にRを追加
• P.117、第二段落1行目：「dN1/dtとdN2/dtは」　→　「dR/dtとdN/dtは」
• P117, 下から5行目：式(3.16)の捕食者の動態をdN2/dt = (-d - bN2 + aN1) N2などと表しても，不自然ではない． →　式(3.16)の捕食者の動態をdN/dt = (-d -δR+ aN)Nなどと表しても，不自然ではない．ここでδは捕食者の密度効果の強さを表す正の係数である。 ☆1行追加　δはギリシャ文字
• P.118、式(3.16)の被食者・捕食者系の-aNの部分を　→　式(3.16)の被食者・捕食者系の-aRNの部分を
• P.136、12行目：数値が変われば間接効果の符号も変わる．捕食者4が1と2どちらを好むかにより結果は変わる．　→　たとえば、捕食者4が1と2どちらを好むかによりさまざまな種間の間接効果の符合と絶対値は変わる．
• P.138、(4.3)式：　dN_idt　→　dN_i/dt
• P.140、(4.7)式の下：の第i行j列要素が，種jの個体数が増えたときに種iの定常個体数が変化する向きと大きさを表している．→　の第i行j列要素は，環境条件pの変化などにより種jの個体数が増えたときに種iの定常個体数が変化する向きと大きさを表している．
• P.144、中央：「表5.1では餌種１だけを利用しているが，餌１の密度を0.1に減らすと，餌２も利用するようになる（補足5.1）。」　→　「表5.1では餌種１と２を利用しているが、餌１の密度を0.2に上げると、餌２は利用しなくなる（補足5.1）。」
• P.175、下から7行目：「=(d/C, CK-d)t/C2K」」　→　「=(d/C, (CK-d)t/CdK)」
• P186,22行目：水俣病は有機水銀に汚染された魚を食べたことが原因だった．
• P.210、表6.2の説明2行目：1行目に示した生起確率が否定されない確率（第一種の過誤
• P211、表6.3の説明2行目：真の確率が0.5のとき，1行目に示した生起確率を受け入れてしまうような高い発生頻度が生じる確率（第二種の過誤）．
• P.217、(6.2)式：r^は　の誤植（＾の部分がv。要するにそのあとの行の説明と同じ記号）
• P.223、(6.19)式の2行前：実際の頻度がf_kであるから（��f_k =12）
• P.223、(6.20)式：【つまり右辺（12!/･･･）の前の12は不要】
  　
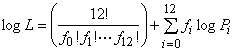
• P.229、問4.1の回答：「シンプソンの多様度指数の…確率を表している。」を削除（互いに異なる種である確率は１−��p_i²である）