
(工事中:不備があればご指摘ください)2016.6.29作成
密度効果とは、個体数N(t)の時間変化が
N(t+1)=R(t)N(t)
のようにあらわされるとき、R(t)とN(t)の間に密度依存性があることです。たとえば
N(t+1)=Exp[r(t)-kN(t)]N(t)
というRicker形の方程式が良く用いられます。ここでkは定数で、r(t)はたとえば平均r*、標準偏差σの正規乱数です。
個体数の対数をとると
log N(t+1) = log N(t) + r(t)-kN(t)
という1次式になります。
まず、こちらのExcelファイルを落手してください。これをもとに説明します。
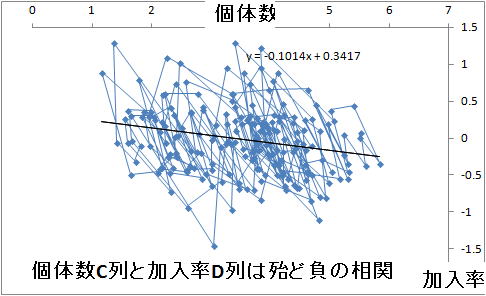
ここでk=0, r=0という密度非依存の時系列を発生させます(t=0~200)。ExcelファイルのセルC3(上記のr*)に0、C5(k)にも0を入れてください。C4(上記のσ)は0.5のままでも、適当な正の値でかまいません。右のグラフはこのときのlog[N(t)]とlog[N(t+1)/N(t)]の相関を見る散布図です。回帰直線の傾きがほとんど負、相関係数(F3)も負になることが分かると思います。しかし、k=0ですから、この時系列は密度効果がありません。この時系列は個々の値が独立ではない(前年の値に依存している)。結果として、発生した200年の期間中で個体数が大きい年には翌年減る傾向があり、少ない年には増える傾向にあります。そうでなければ、もっと個体数が多い年や少ない年があるはずです。つまり、200年間で個体数の多い年というのは無作為の標本ではなく、結果として翌年減る年を選んでいることになるのです。
このような単純な相関では密度効果は検定できません。これで負の相関があるから密度効果があると主張するのは間違いということになります。
まず、調べたい時系列を一つ抜き出します。Excelファイルでは再計算(Functionキー9を押す)のたびにB:C列の時系列が変わってしまうので、BC列の値をGH列に値のみコピーします。普通にコピーすると数式としてコピーされてしまうので注意してください(GH列の網掛けが薄緑から黄色に変わったら失敗です。値のみコピーなら薄緑のままのはずです)。
この時系列=log[N(t+1)/N(t)]<ExcelファイルのJ列>の順番を入れ替えてShaffleした時系列r'(t)を作ります。GH列に値のみコピーしたときに、自動的にK列にできます。再計算するとShaffleし直されて値が変わります。
新たな時系列r'(t)を用いて、新たな個体数の時系列log[N'(t+1)]=r'(t)N'(t)を作ります。この場合、r'(t)は個体数N't)が多いときに小さいという関係はないはずです(Shaffleしている)。ですから、この時系列N'(t)には密度効果はありません。
このShaffleされた時系列N'(t)とr’(t)の相関(セルF5に計算されます)と、元の時系列N(t)とlog[N(t+1)/N(t)]の相関(セルF4にあります)のどちらが小さいかを比べてみればよいのです。もし元の時系列に密度効果があるなら、密度効果がありえないShaffleされた時系列よりも強い負の相関があるはずです。再計算を繰り返してみて、元の時系列の相関のほうが高い試行が20回に1度より少なければ、統計的に有意に、元の時系列に密度効果があることになります。
この時系列は人工的に発生させたので、私たちは答えを知っています。r=k=0で発生させた場合には、F5は頻繁にF4より高くなる(このセルが赤くなります)はずです。しかし、たとえばr=0.4,
k=0.1などとした場合には、ほとんどそうはならないでしょう。
この方法の検定力がどれくらいか、(1)Ricker型とは別のモデルを使ってみる、(2)時系列を200年より短くしてみる、(3)σをさらに大きくしてみる、(4)この場合は観測誤差を無視しているから観測誤差を考慮してみる、(5)過程誤差r(t)が毎年独立と仮定しているがレジームシフトのような自己相関を入れてみる、などをためしてみるのもよいでしょう。
(6)さらに、実際の個体数変動の実例を入れてみるとよいでしょう(その場合、正答はわかりませんが、論理的には密度効果は必ずあるはずだというのが生態学の定説です。密度効果が検出できない頻度を見てみればよいでしょう)
Dennis B, Taper ML (1994)表3 にあるハイイログマの時系列 {33, 36, 34, 39, 35, 34, 38, 36, 37, 41, 39, 51,
47, 57, 48, 59, 64 }、表4にあるイエローストーンのエルク{3172, 4305, 5543, 7281, 8215, 9981,
10529, , 12607, 10807, 10741, 11855, 10768}など
参考文献
Dennis B, Taper ML (1994) Density dependence in time series observations of natural populations:
Estimation and testing. Ecol Monogr 64:205-224.