資源回復計画考え方と注意

齢構造のない変動環境下の個体数変動：N(t)を年ｔでの個体数、λ(t)を個体数増加率とするとき、個体数変化はN(t+1)=λ(t)N(t) で表され、個体数の長期的な消長は、λ(t)の幾何平均が１より大きければ増加、小さければ減少する。
Tuljapurkarの理論： ところが、齢構造などの構造をもつ集団ではそう簡単ではない。たとえば、子供と親の個体数をそれぞれJ(t)、A(t)とするとき、

という行列算で個体数変動が表せるとする。ここでs(t)はその年の親１個体当たりの繁殖率、gは子供が親になる生存率、Gは親が来年も生き延びる生存率を表す。たとえgやGが定数でも、s(t)が変化するだけで、この個体数の消長はいろいろな場合が出てくる。g=0.2、G=0.8でs(t)=２と０を交互に繰り返すとき、個体数は年平均1.9%ずつ増え続ける。s(t)=2の年が続いてからs(t)=0の年が続く場合には、個体数は年平均で4.2%ずつ減りつづける。ところが、この年変動を無視してs(t)=１で毎年一定と仮定すると個体数は増えも減りもしないと予測されてしまう。
このように、生存率や繁殖率が年毎に変化する集団では、変化を無視した平均値を使うと個体数の消長を誤って予測してしまう。変化の自己相関によっても、増加率は異なる。
Tuljapurkar SD (1989) An uncertain life: demography in random environments. Theor. Popul. Biol. 35:227-294.
[D30] 松田裕之・巌佐庸 (1993) 何が絶滅をもたらすのか？：保全生態学の理論,  個体群生態学会会報,  No.50:2-9.

セタシジミの資源回復計画：琵琶湖特産のセタシジミは下図のように、以前は6000トン漁獲されていたが、最近は200トン未満である。これはひとえに網目の細かい魚網による成長乱獲である。セタシジミはおよそ3年で殻長15mmになり成熟し、4年で20mmになる。現在は15mmから漁獲されているが、滋賀県水産試験場では漁獲開始殻長を20mmに引き上げることを提案している。
齢組成模型(age-structured model)と体長組成模型(size-structured model):
体長1mm, 2mm,...,35mmの個体数を列ベクトルn=(n1,n2,...,n35)Tで表す。ｔ年目の個体数組成をn(t)と表す。前年体長ｊだった個体が今年生き残って体長iになる確率をpijとし、前年体長ｊの個体が産む産卵数をe1jとすると、pijとe1jを(i,j)成分とする行列PとE、その和L=P+Eを使って
n(t+1)=L.n(t)
により、個体数変動を表すことができる。（ここではLの年変化は無視する)これを体長組成模型という。齢組成模型では体長のかわりに1歳、2歳、...の個体数列ベクトルにとる。
個体数増加率は体長組成にも左右されるが、Lが毎年一定ならある定常組成に落ち着く。そのときの増加率はLの最大固有値λであり、体長組成はその右固有ベクトルに漸近する。

 滋賀県のセタシジミ漁獲量の年変化(滋賀県水産試験場より)

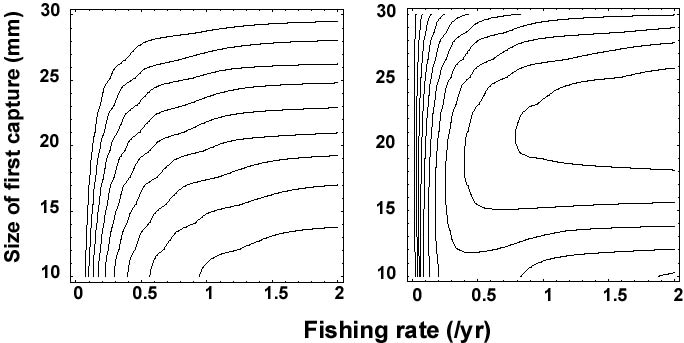
乱獲を表す指標として、YPR(yield per recruit加入あたり漁獲量)とSPR(sparning biomass per recruit加入あたり産卵量)というのがある。下図の左がSPR、右がYPRを、さまざまな漁獲の強さと漁獲開始殻長について描いた等高線図である。左図は漁獲がないときに比べて、ある漁獲開始殻長と漁獲圧のときに1世代が死ぬまでに産み残す卵の数がどれくらい減るか(%SPRという)を表していて、右下の曲線から10%、20%､･･･、90%の等高線を表す。たとえば漁獲圧１で殻長15mm(現在の漁業に対応すると見られる)のときは、漁獲がない場合に比べて20%の卵しか次世代に残さないことを表す。次世代に卵を残さないと加入乱獲を招く。漁獲開始殻長を20mmに上げると、倍の40%の卵を次世代に残すと期待される。
右図は漁獲開始殻長が20-25mmで漁獲圧が高い状況がもっともＹＰＲが高く、再生産を考えなければその世代の資源を効率的に利用していることを示す。現状では15mmから漁獲しているので、成長乱獲であることが示唆される。その意味でも、殻長を20mmに引き上げるべきである。
数学的にはSPRは列ベクトルe.(I-P)-1の第1列で求められる。このeはEの第1行からなる行ベクトル、Iは単位行列、-1は逆行列を表す。
 
セタシジミのYPR(左図)とSPR(右図)
現在の漁業は、10年間で漁獲量が半減していて、毎年7%の減少率である。これを殻長を20mmに引き上げると、逆に毎年数％の増加率が見込まれる。ただし、最初の年は小型の貝を獲らない分だけ漁獲量がかなり減る。
管理元年に漁獲量がどの程度減るか、2年目以降の回復を予測するには、(1)現在は毎年７％で減りつづけている定常体長分布にあると仮定する。(2)管理元年から漁獲開始殻長をXmmに、それより大きな貝への漁獲圧をFにする。 (3)生存率、繁殖率、貝の価格に与える密度効果はすべて無視する。これらの仮定のもとに計算すると、さまざまな管理方針(F,X)のもとで下図のように回復していく。どの(0.955,15)は今までと同じに放置した場合を表し、毎年７％ずつ減っていく。(0.955,20)は殻長を20mmに引き上げる方針を表し、1年目は漁獲量が半減し、2年目には3割減に回復し、その後は放置したときよりも高い漁獲量がえられるが、管理前の漁獲量に回復するのは8年目のことであり、20年後に漁獲量が倍増すると見込まれる。
 
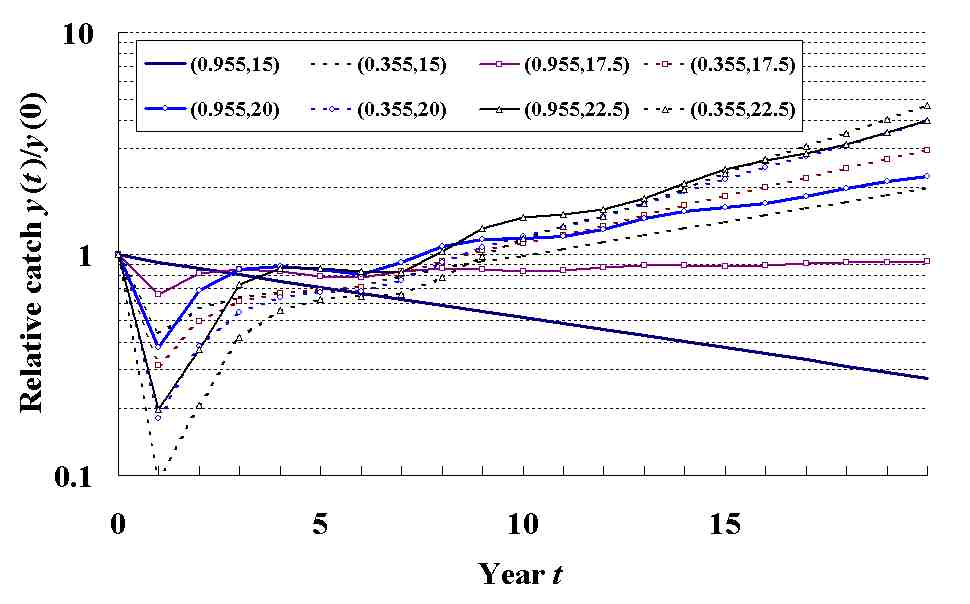
このように漁獲開始年齢(体長)を引き上げて加入乱獲を防ぎ、資源を回復させて漁獲量を回復させるには、かなり長い年月を要する。一般に(1)引き上げる漁獲開始年齢の幅が大きいほど管理元年の漁獲量の落ち込みが激しい。(2)体長組成(齢組成)が管理後の漁獲圧のもとで定常分布に達するまでには、世代時間の長い生物ほど長い時間(世代時間の2,3倍)がかかり、その間は漁獲量は定常環境でも振動を繰り返し、順調には増えていかない。これはミナミマグロでも同じである。(3)最終的な漁獲量(資源量)上昇率は、管理後の行列の最大固有値に一致し、開始年齢が高く、漁獲圧が低いほど高くなる。